Rotational Inertia of Solid Bodies

A solid body is made up of a number of particles. We can calculate its rotational inertia by taking the sum of the rotational inertias of each particle.

To do so, imagine the body divided into a large number of small mass elements each located a perpendicular distance from the axis of rotation. Our rotational inertia is:

If we make the size of each mass element smaller and smaller, we can transition to calculus:

We can use this to create varying formulas for different types of solid bodies.

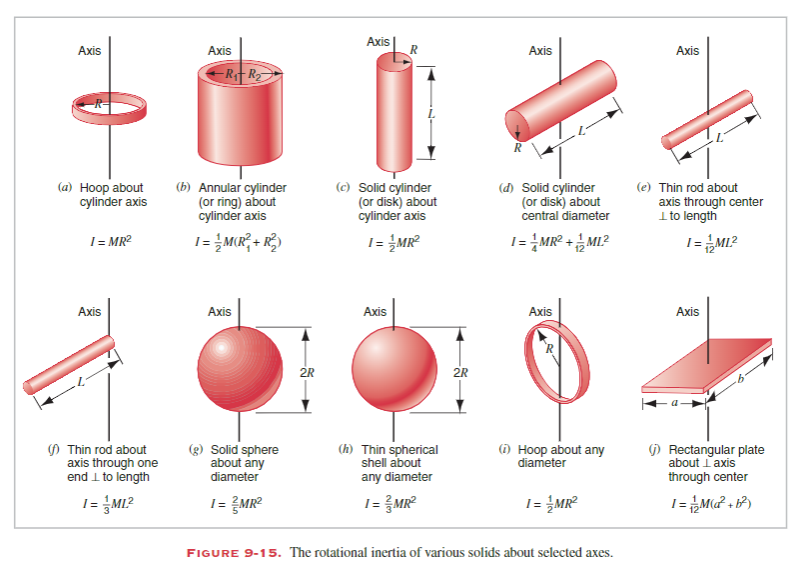
For example, for a rod:

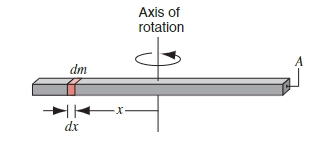
The rod has a length , cross-sectional area , and uniform density .

If we want to rotate the rod about its end, use the Parallel Axis Theorem substituting this for .

Or for a plate:

We can divide the plate into a series of strips where we consider each to be a rod.

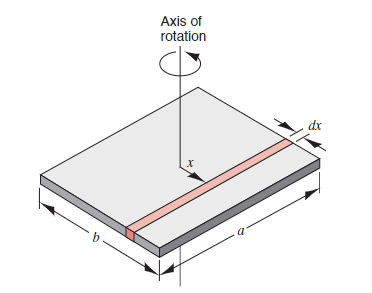
Note that the plate has extremely small height; this picture shows a large amount.

The mass of the strip is related to total mass like how the surface area of the strip is related to the total surface area :

The rotational inertia of a strip about its Center of Mass is :

Substituting for and for :

Taking the integral from to :

We can continue using this method for a cube using a stack of plates, etc.