Variation of Pressure for Fluids at Rest

On this page, we will look at fluids in Equilibrium, meaning that every portion of the fluid has both net force and net Torque equal zero.

Consider a small portion of fluid within the greater body of a homogeneous fluid. The element should be shaped like a thin disk with height and area .

The mass of the element would be:

and the weight would be:

The disk has no horizontal forces, and since the element is at equilibrium, its vertical forces must be net zero.

Lets define some more variables:

• is the pressure on the lower face.
• is the pressure on the upper face. We add the due to change in pressure from the height .
• is the upward force on the lower face since .
• is the downward force on the upper face for the same reason.

So, for the vertical forces:

From which we get:

We can use this equation to tell us how pressure changes from elevation above a certain point.

Info

is also known as the weight density of a fluid, the weight per volume of a fluid.

We can integrate this to find pressure at a certain point:

Liquids rarely compress, so we can keep constant as we integrate.

We can manipulate the equation further for instances where the liquid is being held in a regular container, such as a beaker:

The pressure is dependent on the depth, , below the surface.

For more weirdly shaped containers, we use our original equation, . This equation can be used to find the difference in pressures for any two points. For example, for a U-tube:

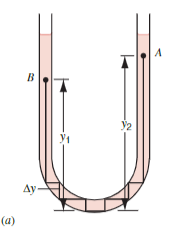
For the change in pressure between points A and B, we just sum the vertical segments between A and B and multiply it by .

Variation of Pressure in the Atmosphere

For gases, the density, , is relatively small, so the difference between two points is negligible. As a result, for a gas in a container we can say the pressure is the same everywhere. Yet if the distance is great enough, such as in earth’s atmosphere, matters and pressure changes.

We can get a good idea for this by assuming density is proportional to pressure.^[Normally this is the case, but for the atmosphere temperature also matters.]

Since density is proportional to pressure:

Using this:

where . and are the pressure and density at sea level, so is a constant.

Note that the pressure drops by a factor of . In other words, the atmospheric pressure drops by a factor of when the altitude changes by .