Distributed Charges on Objects

If we have a distributed charge on some object, the principle for calculating values such as Coulomb Force, Electric Field, etc. related to the object is to first split up the object into portions, then find the value from each of those portions.

If we have some object and we want to find the Coulomb force on point outside the object, then we can break the object into pieces and calculate from each the charge of the object.

By splitting into an infinite amount of portions, we can arrive at

In order to calculate the total charge, we need to charge density function All it does is tell us how charges are distributed over space. We often use different notations for different types of densities.

• Volume Density . .
• Surface Density .
• Line Density . .

It is from here that we can integrate over the entire object.

For example, take a wire of charge of length and charge distributed according to function where is a known constant. How can we find the Coulomb Force at some point with charge away from the wire?

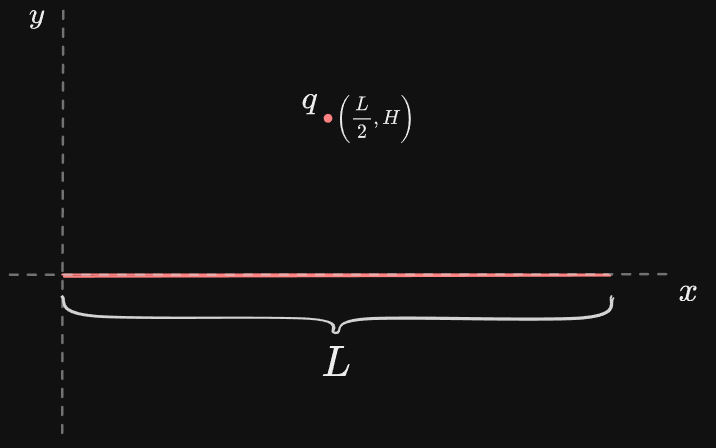
We impose a coordinate system on the object and integrate from to .

We will do two substitutions here.

So our integral is

We find ,

So our integral is

The final solution for this integral is