LR Circuits

An LR Circuit is a Circuit with an Inductor and Resistor. Here is an example of (a) a disconnected circuit, (b) the same circuit with 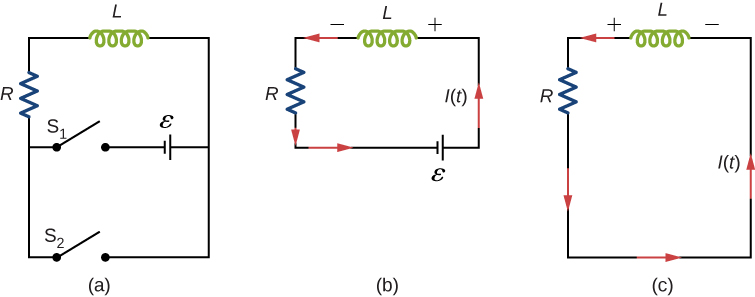closed, and (c) the same circuit with open and closed so that there is no battery powering the circuit

When the configuration changes from (a) to (b), the current increases from 0 to at a slower speed than if there were no inductor. When the configuration change from (b) to (c), The current should normally quickly drop back to 0. However, because the inductor resists changes in current, it takes time to do so, and there would still be current moving over the resistor during that time. In this way Inductors are similar to Capacitors and RC Circuits.

Let’s create a function for the change in current. We start off using Kirchhoff’s Laws to analyze the circuit and moving from there. First, during charging in position (b):

We can also define the final current , and the time constant :

Using the equation from before, we can also calculate the potential difference across the resistor.

And potential difference across the inductor:

Now lets find the equation for discharging:

The potential difference across the resistor:

and across the Inductor:

For AP Physics C students, make sure you know how to graph each of these equations.