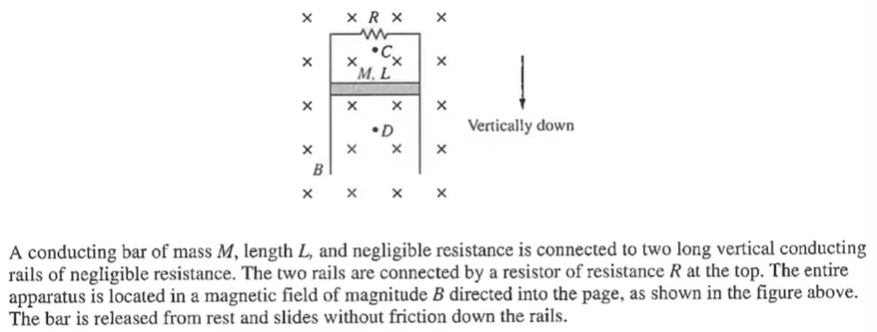
Question
Since the area of the loop increases as the bar moves, the Magnetic Flux increases. Per Lenz’s Law, a magnetic field opposite to that of the current Magnetic Field is induced. In other words, the magnetic field into the page decreases. Using the Right-hand Rule for Rotation, we can find that there is a counter-clockwise current, and that the direction of the current in the resistor is left.
Question
bi) Is the magnitude of the net magnetic field above the bar at point
greater than, less than, or equal to the magnitude of the net magnetic field before the bar is released?
It is less than. the magnetic field into the page decreases as an induced magnetic field opposing the current magnetic field is created by the increasing magnetic flux.
Question
bii) While the bar is above point
, is the magnitude of the net magnetic field at point greater than, less than, or equal to the magnitude of the net magnetic field before the bar is released?
Greater than. Recall that the magnetic field loops around a current carrying wire. As a result of this fact, the magnetic field induced outside the loop will be pointing downwards, increasing the net magnetic field into the page.
Express answers to part (c) and (d) in terms of
Question
c) Write but do not solve a differential equation that could be used to determine the velocity of the falling bar as a function of time.
Question
d) Determine an expression for the terminal velocity
of the bar.
Terminal velocity occurs when the acceleration is zero.
Express your answers to part (e) and (f) in terms of
Question
e) Derive an expression for the power dissipated in the resistor when the bar is falling at terminal velocity
Question
f) Using your differential equation from part (c), derive an expression for the speed of the falling bar
as a function of time.