AP Physics C — LR Circuits Questions

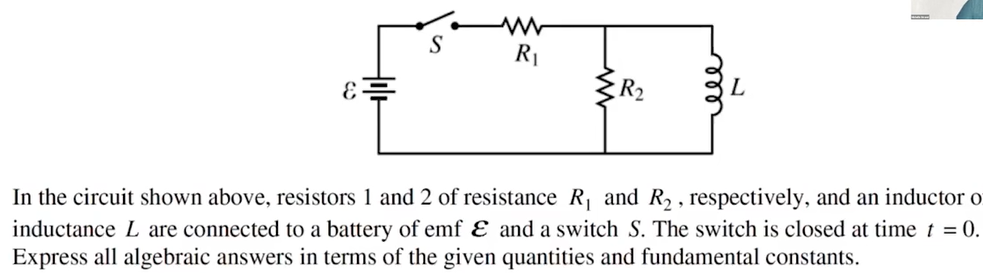
Question

Determine the current through Resistor 1 immediately after the switch closes.

The current through the Inductor is zero because it resists change in current. So we use Ohm’s Law for just the resistors:

Question

Determine the magnitude of the initial change in current in the inductor.

Since Resistor 2 and the Inductor are parallel, we can set their Voltage equal to each other.

Question

Determine the voltage through the battery a long time after the switch is closed.

Current will flow through the Inductor rather than the resistor because the Inductor has much less resistance (a now negligible amount) than the resistor. So, we can just use Ohm’s Law with R1.

Question

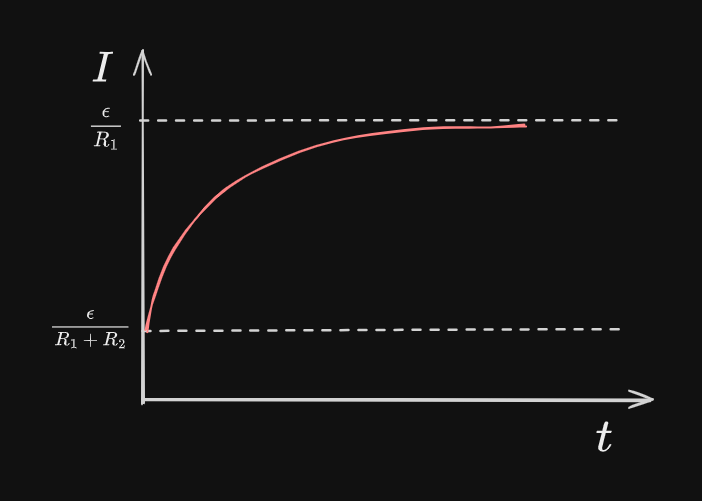
sketch a graph of the current as a function of time

Question

Some time after steady state, the switch is opened. Determine the voltage across resistor 2 just after the switch is opened.

We start by using the steady state current from the inductor.

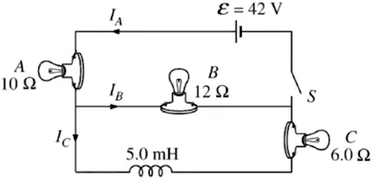
Question

Determine , , and immediately after the switch is closed.

Because the inductor resists change in current, . So, we can use Ohm’s Law for the rest:

Question

Determine , , and a long time after the switch is closed.

After a long time, the voltage across the inductor is 0. For switch A:

splits into and . Since the resistance in is twice as much as the resistance in , the current in is half as much as in . So, and .

Question

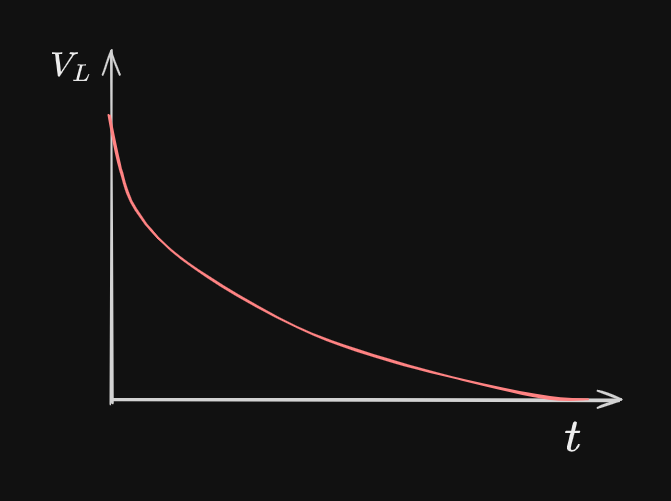
Sketch the magnitude of the potential difference across the inductor as a function of time, from immediately after the switch is closed to a long time after the switch is closed.