AP Physics C — Moving Loop Problems

We will use Newton’s Second Law, Faraday’s Law, and Lenz’s Law to analyze a conductive Bar’s Motion on rails.

The loop of wire below has width 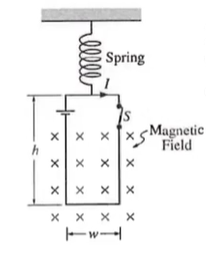, height , and contains a switch and a battery. It is connected to a spring of force constant . The loop carries a Current moving clockwise and the loop’s bottom has a uniform magnetic field pointing into the page.

Question

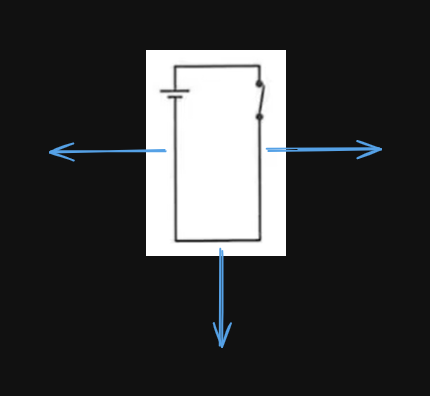
a) Indicate the direction of the magnetic forces that act on each side of the loop.

Question

b) The switch is opened and the loop eventually comes to rest at a new equilibrium position that is a distance from its former position. Derive an expression for the magnitude of the uniform magnetic field in terms of the given quantities and fundamental constants.

Since the loop has come to rest, the net force must be zero. So, the spring force and magnetic force must be equal (we say gravitational is negligible)

---

The spring and loop are replaced with a loop of the same dimensions and Resistance 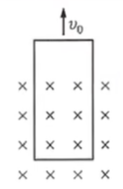but without the battery and switch. The new loop is pulled upward, out of the magnetic field at a constant speed . Express algebraic answers to the following questions in terms of , , , and the dimensions of the loop

Question

c) Indicate the direction of the induced current in the loop as the loop moves upward.

If we are pulling the loop up, then the area overlapping with is decreasing, so flux is decreasing. Therefore, a new magnetic field is created in the same direction as the current magnetic field, and into the page increases. Using the Right-hand Rule for Rotation we can find that the direction of induced current is clockwise.

Question

Derive an expression for the magnitude of this current.

We can use Faraday’s Law:

Question

d) Derive an expression for the power dissipated in the loop as the loop is pulled at constant speed out of the field.

Power is . In this case we use Electric Power .

Question

Suppose the magnitude of the magnetic field in increased. Does the external force required to pull the loop at speed increase, decrease, or remain the same?

. If increases, then increases. Therefore, to keep the loop moving at , a larger force applied must be used.