Vectors

A vector is a point with a direction. Oftentimes, they are represented by an arrow. They are also represented as a list of numbers (or other stuff, like functions).

When it is a list of numbers, we can think of it as an arrow in space. For example, we visualize the vector  as an arrow whose tail is at the origin and whose tip is at the point .

Sometimes we draw the vector with the tail not on the origin. The vector shifted up so that it starts at is still called the vector.

This is why it can sometimes be confusing to have vectors act like points in space.

Notation

Three ways to write vectors:

For , the arrow is a convention that shows that it is a vector.

• The first notation is the point notation, which can extend to any number of dimensions
• The second notation is Matrix notation, which can also be extended to any amount of dimensions. This notation is useful when vectors interact with matrices.
• The third notation only works in 2D and 3D. It uses Unit Vectors (“I-hat”), , and
  • and is the unit vector.
  • and is the unit vector.
  • and is the unit vector.

We usually use the first notation in exercises

Vector Addition

In general, whenever we add two vectors, we add their corresponding components.

We can visualize this as:

Scalar Multiplication

This is when we stretch or shrink a vector by a Scalar, which is just a regular number.

In general, this just means we multiply each component by the scalar.

When we multiply a vector by -1, we flip the vector.

Magnitude

We write the magnitude, or length, of the vector like or .

We can calculate the magnitude with the Pythagorean theorem.

Dot Product

The dot product of two vectors is a number that tells us how much two vectors point in the same direction.

In simple terms, it is the magnitude of both vectors times the cosine of the angle between the two vectors.

When , the vectors point in the same direction. This is when the dot product is at its largest, because .

When , the vectors are perpendicular to each other.

When , the vectors are opposite each other.

We usually have to compute the dot product a lot. Therefore, a shortcut is to multiply corresponding components and then add.

This formula extends to vectors of any length.

Cross Product

The cross product between two vectors returns another vector. A vector where has two properties.

1. is perpendicular to both and . In terms of the dot product, we can say that

This also means that the cross product only works in three dimensions. In four dimensions, there are infinitely many vectors perpendicular to two vectors (Think of it as a line of perpendiculars). 2. The length of is a measure of how far apart and are pointing, augmented by their magnitudes.

It looks like the dot product with a sine instead of a cosine. Because of this, when the angle is 90 degrees, the cross product is largest. This makes the dot product and cross product complement each other.

One interpretation of the length of is very useful.

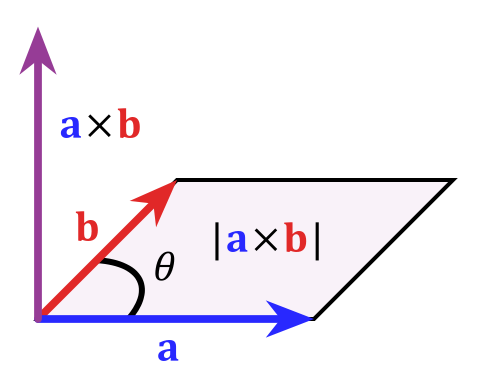
The base of the parallelogram has length and the height has length . The area of the parallelogram is the magnitude of the cross product (base times height).

The Right-hand Rule

You might have noticed that in a three-dimensional plane, there are actually two ways a third vector can be perpendicular to two other vectors. In order to decide which one, we use the Right-hand Rule.

Cross Product Formula

For:

The cross product here is a 3D Determinant.