Gravitation

The law of gravitation is an Inverse Square Law meaning that it varies proportionally to a distance squared.

The force of gravity is:

Where is the gravitational constant,

and are the mass of two objects, and is the distance between their centers of mass.

In terms of Vectors, our law is:

and

Where is a unit vector with magnitude that only specifies the direction from the other mass to this mass. We have a negative sign because we are indicating that the force is opposite the direction from the other mass to this mass.

This is what the subscript represents.

• the force of on , a vector pointing from to .
• represents the distance from to , a vector pointing from to .

And vice-versa for 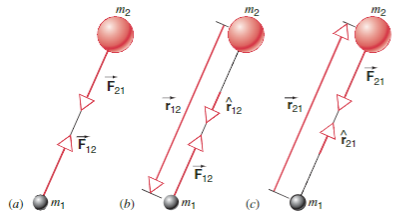and .

Note that .

When there are more than two bodies, we can add vectors to find the total gravitational force for a mass.

For gravitation near the earth’s surface, we often use the free-fall acceleration from gravity . With Newton’s second law:

Many times we assume that , but acceleration due to gravity does change depending on the distance from the earth’s surface. Combining the above equation with Newton’s law of gravitation:

Where is the mass of the earth.

There are also more irregularities:

1. The density of the earth varies from point to point
2. The earth itself is approximately an ellipsoid, not a sphere.
3. The earth is rotating, shifting those irregularities constantly and creating a centrifugal force that varies based on latitude.

It is difficult to take the mass of every particle on earth and sum the gravitational force vectors from each to find a good gravitational force. However, using the first Shell Theorem:

Transclude of The-Two-Shell-Theorems#c89bad

We can represent the earth as a point mass located at its center (Its Center of Mass).

The distance from to is from the center of each mass, not its surface.

Gravitational Potential Energy

Escape Speed

The Motions of Planets and Satellites