The Two Shell Theorems

Oftentimes we can use the two shell theorems to simply the analysis of forces following an Inverse Square Law. The shell theorems state:

Shell Theorem 1:

A uniformly dense spherical shell attracts an external particle as if all the mass of the shell were concentrated at its center.

Shell Theorem 2:

A uniformly dense spherical shell exerts no gravitational force on a particle located anywhere inside it.

Proof of the Shell Theorems:

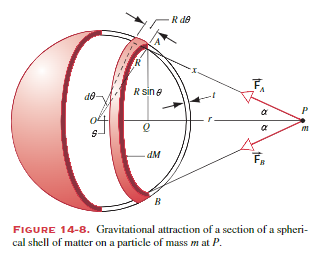
Lets use the gravitational force for this example.

We have a shell of total mass , thickness , and uniform density , and a point mass at point a distance from the center of the shell.

We also have a very very thin ring of width . Because the ring is so thin, every particle on the ring is a distance from . An example particle on the ring at point exerts a force on m, and another example particle at point exerts a force on . Both forces have equal magnitude and their sum lies on the line , which is also true for any other two opposite particles on the ring.

For an element of mass at point A, the component of force along is:

For extending this for every mass element in the ring:

Getting the volume from the mass, then using it to find total mass:

• The ring has dimensions
• is the circumference of the ring.

Lets plug this into our equation for :

Using law of cosines for triangle to get an expression for gets us:

Which we differentiate for to get:

We can also take law of cosines with , giving us:

Substituting these into the equation for gives us:

To get the total force, take the integral:

Where is the radius from the center of the shell, proving shell theorem 1.

When we apply the method method above for , note that .

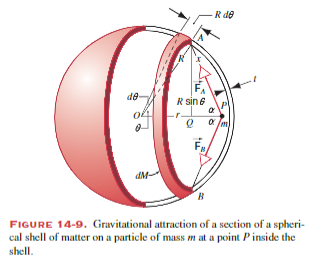
As a result, when you take the integral from the inside of the shell, the result will be zero, proving shell theorem 2.