Centripetal Acceleration

A spinning object has a centripetal acceleration towards its axis that keeps it spinning. Even if the speed at any time is not changing, the direction is, meaning that there is a change in velocity over time, and therefore an acceleration.

We can obtain an equation for centripetal acceleration using the equation for linear acceleration in terms of polar coordinates (see Rotational Motion).

Assuming the radius is constant, we get

Since centripetal acceleration is only radial, we get

Why is this negative? is outwards, and centripetal acceleration is inwards towards the center. We can also write this as

We can also find the same result using a different method. Acceleration is defined by:

However, our velocity doesn’t only change by magnitude, but also by direction.

Let’s assume we have an acceleration of constant magnitude. By taking a very small change in 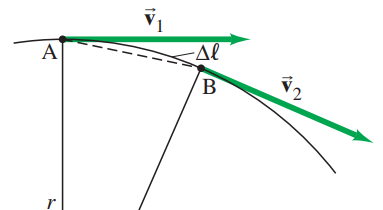along the circumference over a very small , we get:

Our is the difference between these two velocities, so:

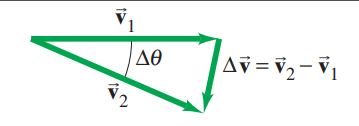
As becomes increasingly smaller, will become almost parallel to and will point towards the center of the circle. As a result, will also point towards the center of the circle.

Since we are only focusing on direction and not magnitude, we will have it be different from normal angular acceleration and call it centripetal acceleration .

We can calculate the magnitude of centripetal acceleration. Take and to be extremely small and since the magnitude does not change (note that does not have an arrow—this is a magnitude), we can write:

Using centripetal acceleration, we can get a Centripetal Force.