Rotational Motion

Sometimes we encounter situations where there is an object moving about an axis. The simplest method to handle these cases is to introduce a circular coordinate system

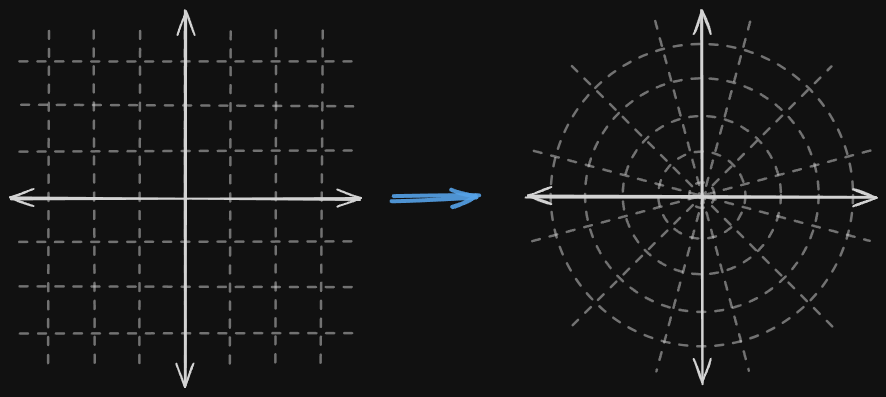
We turn our rectangular coordinate system using an and axis into a polar coordinate system based on radius and angle with some respect to some direction (typically the -axis) . A point in rectangular coordinates is in polar coordinates. In general, polar coordinates are written . Note that some and . The arclength along a circle of radius is .

So a vector in polar coordinates will be described as , unlike in rectangular coordinates where vectors are described . To convert we do:

Note how is the derivative of with respect to ! Wow! Sigma!

Some variables:

Angular velocity is also denoted and angular acceleration is also denoted . We can also use the following equations to equate angular acceleration and velocity to rectangular acceleration and velocity.

Since

This makes sense. Imagine two points on a spinning record, one closer to the center of the record and one farther. Even though entire record has the same angular velocity and acceleration, the point at the center of the record moves a smaller distance in the same amount of time as the point farther from the center. So the point closer to the center has a smaller velocity because its distance from the center is smaller.

However, this is only the case for a pure angular acceleration and velocity. If we introduce a radial velocity and acceleration, we get much more complicated equations.