Angular Momentum and Angular Velocity are not always parallel, and this is evident in three-dimensional cases. Take this example:
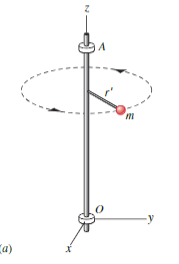
A particle of mass is attached to a rigid massless shaft by length and it moves at a circle with constant speed .
The only force that acts on the particle is the Centripetal Force from the arm. We don’t consider gravity to keep things simple.
Using Right-hand Rule for Rotation the angular velocity points up parallel to the axis.
The angular momentum of the particle is given with respect to the origin . This means the radius we use is and not .
Look at in the picture below. We fine using the Cross Product, so does not point in the same direction as .
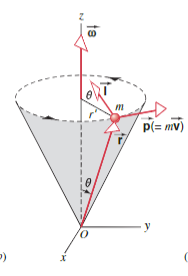
Lets focus on the components of , specifically in the direction, .
Substituting for :
is the Moment of Inertia of the particle in respect to the axis:
Our angular velocity only applies to the component of in the direction. We know this from our initial equation:
This result also means that our changes direction over time as the particle spins around the shaft.
The other part of causes Torque due to Angular Momentum.

