Angular Momentum

Momentum also has a Rotational Motion analog, Angular momentum :

Newton’s Law can be written as

Similarly:

We can derive this:

The analogy from translational to rotational carries over in other ways.

To specify direction for , use the Right-hand Rule for Rotation. This looks like:

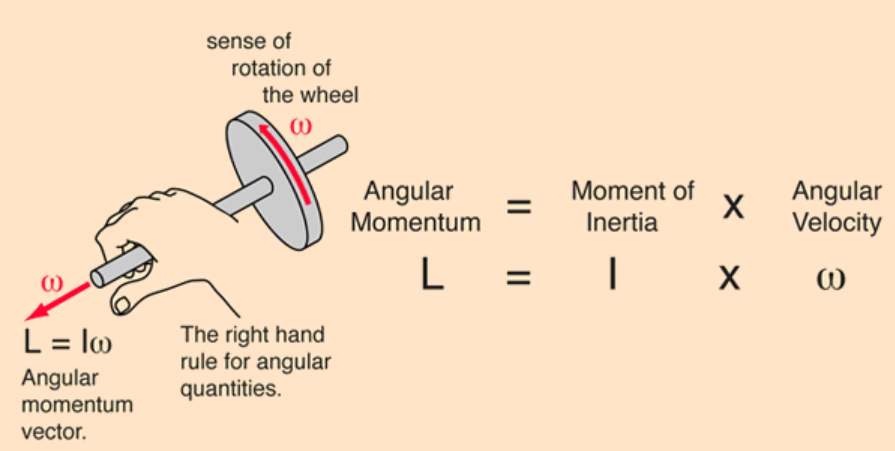
We can compare this to linear momentum:

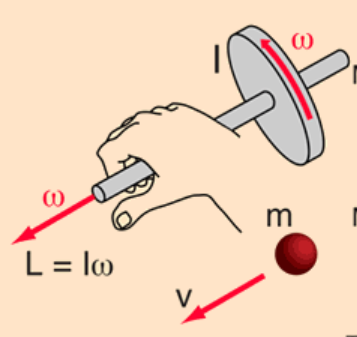
Suppose we have a force acting on a particle with momentum which as a result changes by . Lets say that is very small.

When is parallel with , the momentum of the particle changes to . When is perpendicular, the momentum of the particle changes to , but since is so small, the only effect is a change in direction.

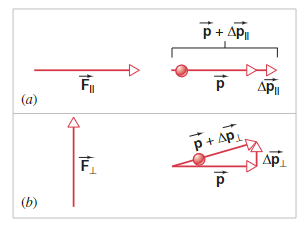
A similar phenomenon occurs for rotational movement. When is parallel with , the momentum of the particle changes to . When is perpendicular, the momentum of the particle changes to , but since is so small, the only effect is a change in direction.

Using this principle, we can show an interesting phenomena:

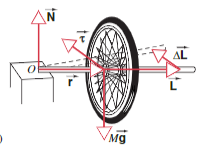
Because the torque of the wheel is perpendicular to the angular momentum, the axle moves.

There is also a law for Conservation of Angular Momentum where is constant. This causes many interesting phenomena to occur. For example, as decreases, decreases, meaning that must increase.

For Conservation of Angular Momentum to be sustained, net Torque must stay the same, but the Force does not. The object can undergo translational motion without introducing an outside torque to the object.

Angular Momentum and Angular Velocity