Streamlines and Tubes of Flow

Streamlines

In steady flow, the velocity of a given point is constant in time — meaning that does not change. As a result, every fluid particle arriving at will move with the same to get to the next point, following a fixed path. This path is called a Streamline.

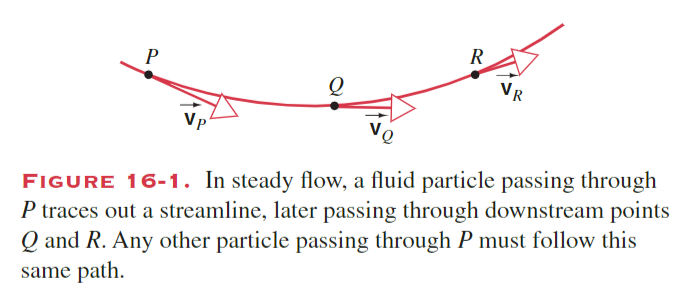
• The magnitude of the velocity vector is always tangential to the streamline.
• No two streamlines can cross each other. Otherwise, fluid particles may have a choice on whether to go on one path or another path, meaning that it would not be fixed.
• In principle, we can draw a streamline through every point in the fluid.

Tubes of Flow

By bundling streamlines together, we can create a region called a tube of flow.

• No fluid can cross the boundaries of a tube of flow.
• The fluid that enters at one end must leave the other.
• Typically when defining a tube of flow, we do it so that the tube is narrow enough so that the velocity is nearly constant over a cross-section.

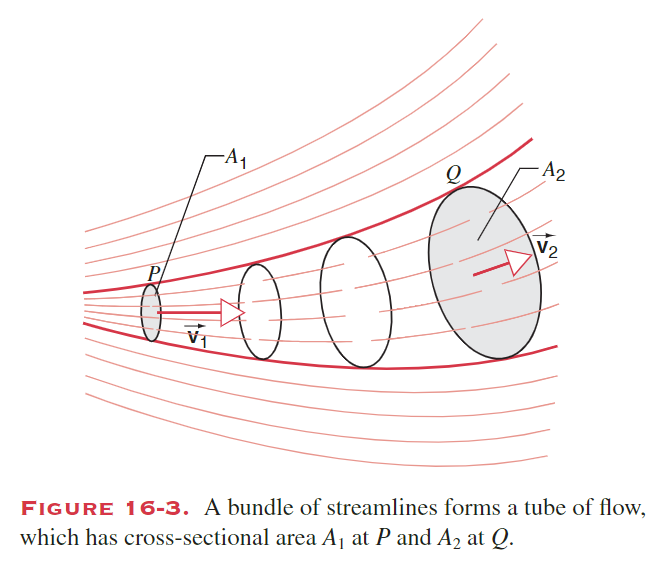
In the image above:

• Fluid enters at with cross-sectional area and leaves at with cross-sectional area .
• Fluid particles at have velocity and fluid particles at have velocity .
• During an amount of time a fluid element travels distance .
• The fluid that crosses during has volume .

If the density at is , then the mass of fluid is:

We can use this to find mass flux, the mass of fluid passing through a cross section per unit time. At this is approximately:

To get this value precisely, we must take the limit at approaches so that the area does not change too much.

With the conditions that the flow is steady and there are no other sources or sinks, the fluid mass enters the tube at the same rate that is leaves it. As a result:

or:

This expresses the Law of Conservation of Mass in fluid dynamics.

If the fluid is incompressible, then the density remains the same:

or defining as the volume flow rate:

has units .

Equations and are called the Equations of Continuity for one dimensional flow.