Viscosity

Viscosity in fluid flow is similar to the concept of friction. If we want to keep a body at a constant velocity, we must have an external force to counteract the friction.

We can apply a similar logic to fluids by envisioning them as a series of plates.

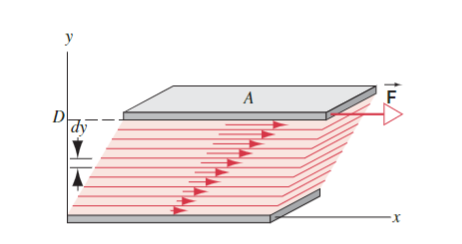
In the example, a force is applied on the top plate so that it has constant velocity compared to the bottom plate. counteracts the viscous drag not only between the top plate and the fluid, but within the fluid itself. That is why we use the plates to specify that effect.

The speed of each layer differs by a , making this an example of laminar flow — one that uses Streamlines and Tubes of Flow.

We know that the area of the top plate and each of the layers will have an effect on how much viscous drag there is, and thus the force that we apply. We will thus say that force is proportional to the area times change in velocity that results from a change in the height of the layer. In mathematical terms, this is:

or, using as a constant of proportionality:

is the coefficient of velocity and it varies from fluid to fluid.

In the case for the rectangular layers above, the velocity gradient is constant, so we would instead write:

For a more practice example, we can look at viscosity in pipes.

In this case, our layers are not rectangular but cylindrical with varying radii. Assuming that the layer next to the walls is at rest, the speed in a shell of radius is:

Which depends on the pressure difference across the length of the pipe. The speed at the center of the pipe is:

Using more derivation, we can show that the total mass flux is:

This result is Poiseuille’s Law.