Ampere’s Law

Quote

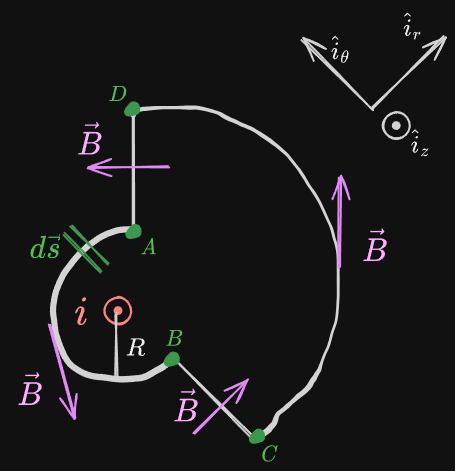
Ampere’s Law states that for any closed loop path, the sum of the length elements times The Magnetic Field in the direction of the length element is equal to the permeability times the electric Current enclosed in the loop.

We use imaginary Amperian loops to determine the magnetic field from a surface. It is similar to Gauss’s Law.

The Differential Form of Ampere’s Law is

This is not actually Ampere’s Law! Maxwell added a term for Displacement Current, so the complete Ampere’s Law is

Some examples:

Along a Long Straight Current Carrying Wire:

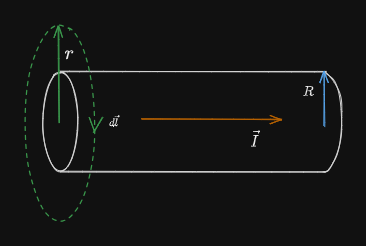
We form an Amperian loop (green) with radius in direction around the wire with radius with current . We then use Ampere’s Law:

Inside a Long Straight Current Carrying Wire

This is the same as before, but this time .

Since we aren’t using the whole current and only a portion, we have to use Current Density for .

We use this in Ampere’s Law:

Radially Shaped Wire