Displacement Current

Displacement Current is Maxwell’s addition to Ampere’s Law.

For the capacitor below:

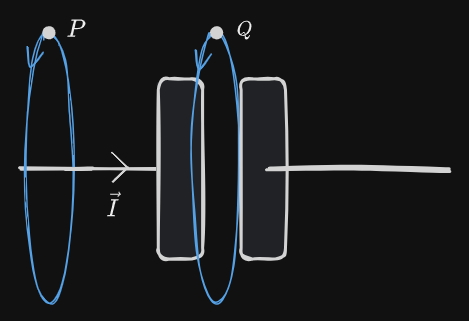
We can find The Magnetic Field at point using Ampere’s Law. We form an Amperian Loop around point and see that the Current enclosed is , and that therefore there is a Magnetic Field at .

Between the two plates there is no current, so when we form our Amperian loop, there should also be no Magnetic Field at point . However, observational evidence says otherwise. A Magnetic Field does form between the currents. In fact, the magnetic field at equals the magnetic field at point .

This means that Ampere’s Law is missing some component, and Maxwell was able to find that component. He reasoned that if a change in Magnetic Flux created an Electric Field, then a change in Electric Flux created a magnetic field. The complete equation would be:

The is the conduction current and is the displacement current.

The derivation for this is as follows. We start by using Gauss’s Law over the positive plate of the capacitor:

Then we look at the charge of the capacitor:

Then we look at the capacitance:

And plug it in: