AP Physics C — Magnetism and Current-Carrying Wires

Deriving the Equation

Since Charge in a Magnetic Field Experiences a force , we can use this on the moving charges (Current) in a wire.

Let’s derive the equation for the force on a wire.

First, we need a measure for the amount of charge. We say:

Where:

• is the number of charge carriers per volume.
• is the cross sectional area of the wire.
• is a certain length of the wire.
• is the charge per carrier

Then we use a couple of different equations:

Which gives us an equation for force from to . We can use the Right-hand Rule to figure out the direction of the force from the Cross Product. For a straight wire, is constant, so we just use:

Torque on Looped Wire

For a looped wire configured as below, there will be magnetic forces outwards from each wire. You can check this using the Right–Hand Rule.

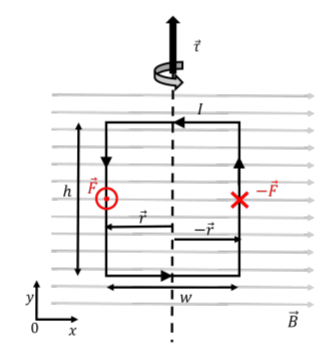
For an axis moving along the direction of the first part of the wire, we can calculate the Torque:

Giving us an equation for the torque on a wire in a magnetic field.

Magnetic Field around a long current-carrying wire

We can use Ampere’s Law to find this equation:

Transclude of Ampere’s-Law#along-a-ap-physics-c--magnetism-and-current-carrying-wires-magnetic-field-around-a-long-current-carrying-wire-long-straight-current-carrying-wire

How can we calculate the magnetic field from multiple wires at a point ?

1. Calculate each wire’s magnetic field on .

2. Use the Right-hand Rule for Rotation to determine the direction of on . (Excuse my poorly drawn hand)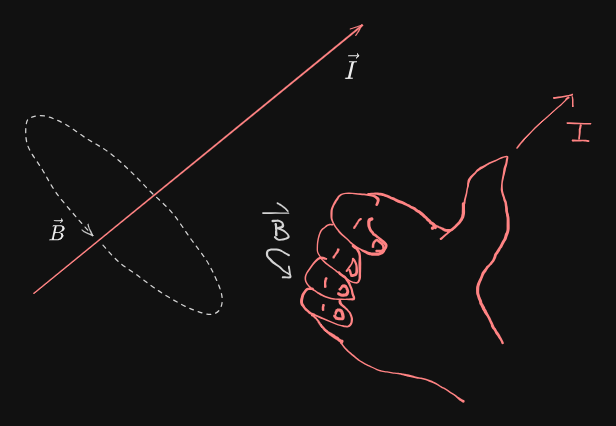

3. “add” the vector quantities and calculate the final magnitude and direction.

For example

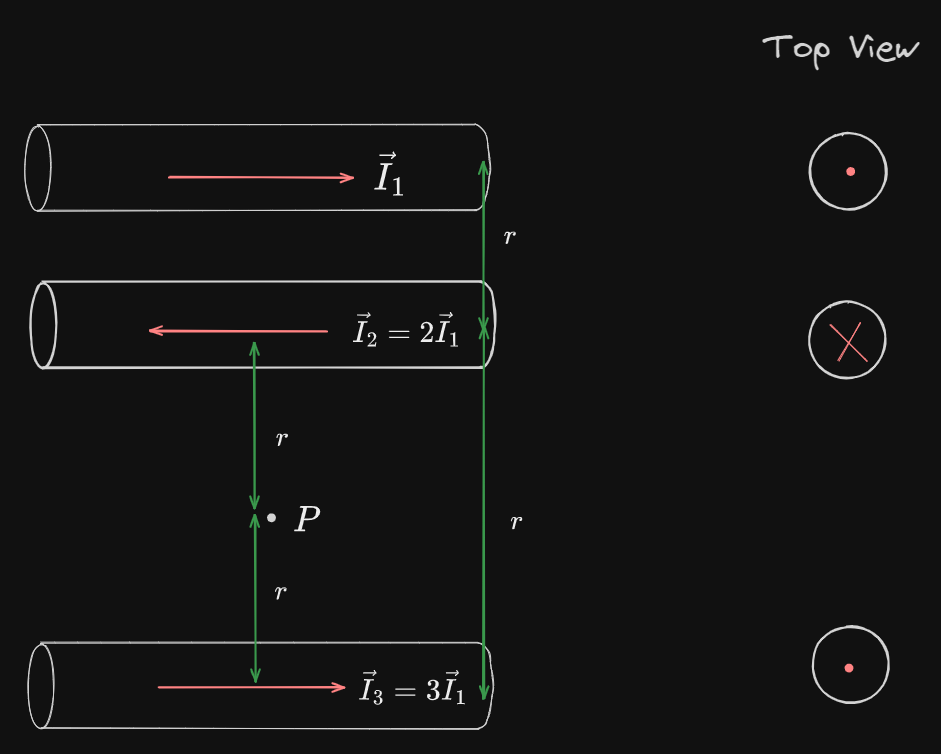
Answer

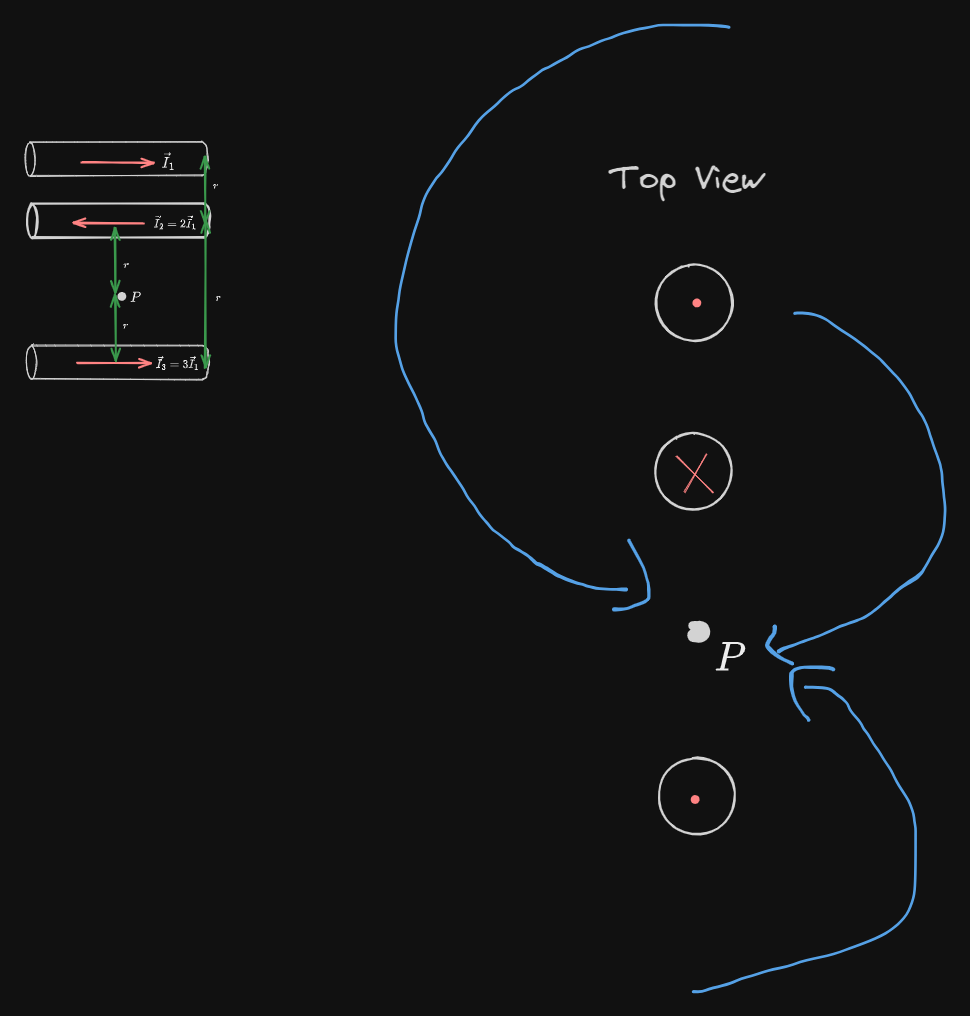
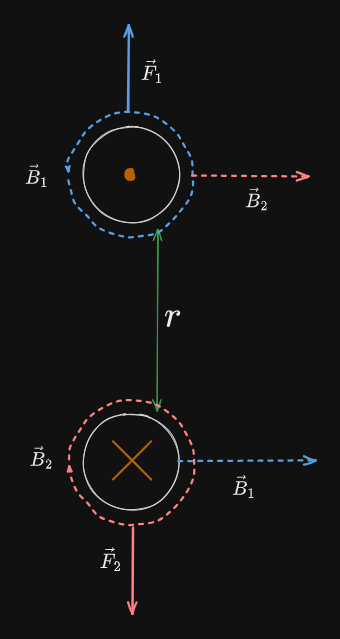
For the magnetic force from two parallel current carrying wires:

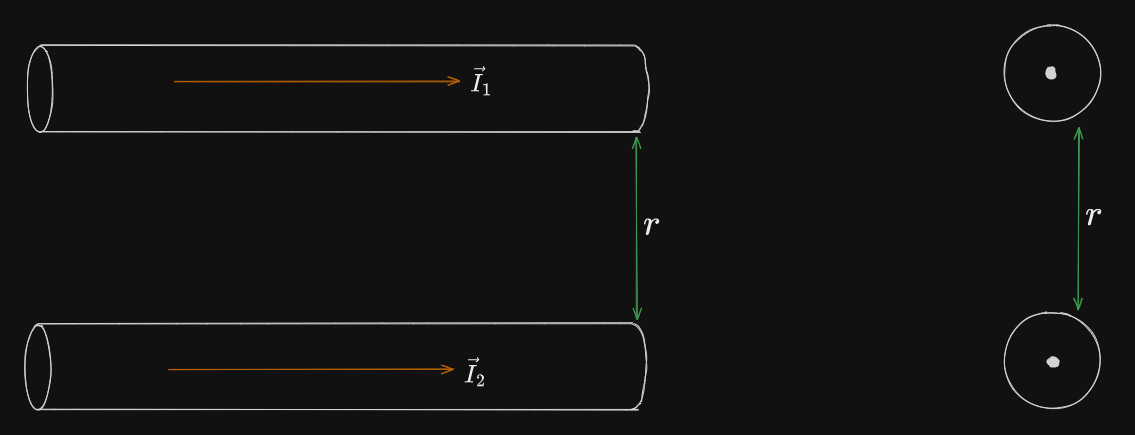
We use the rotational right hand rule and reason the magnetic field of each wire on the other: 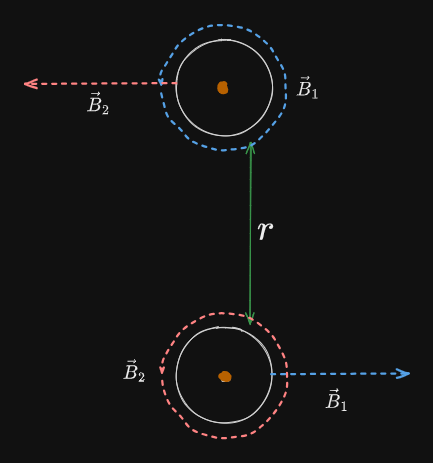We then use the regular Right-hand Rule to reason the Magnetic Force:

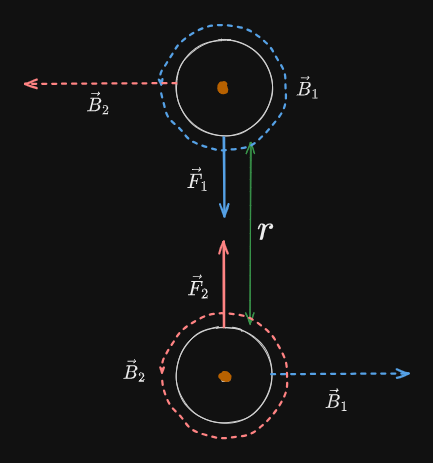
Then we calculate:

It makes sense that the magnetic forces of two wires on each other equal one another because of Newton’s Third Law: that every action has an equal an opposite reaction.

If the currents are moving in opposite directions:

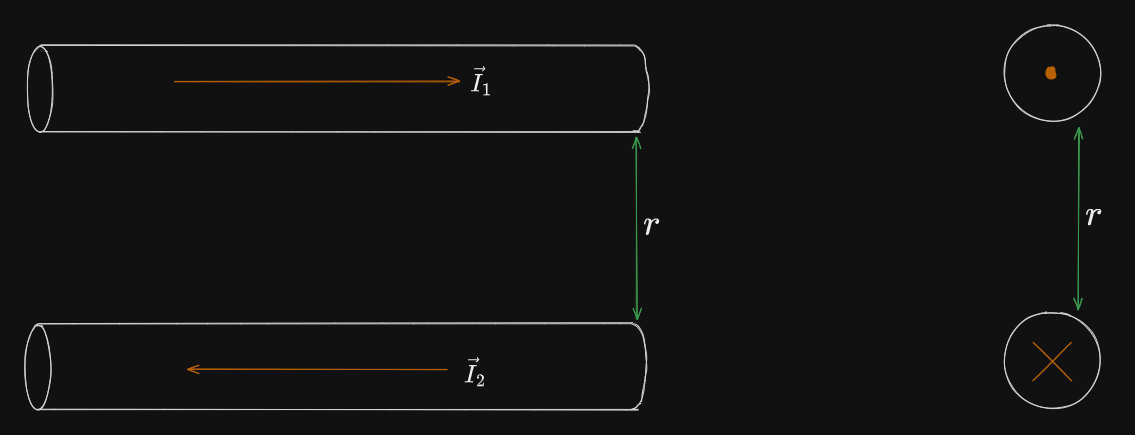
Then we use the same process:

The force is the same:

This equation is also seen as the force per unit length:

Wire attract when current is in the same direction and repel when they are in opposite directions.