Center of Mass Energy

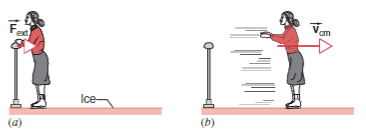
Lets use the example of a skater pushing herself off the railing of an ice rink. The skater cannot be represented with a single particle, as her arms and body move differently, so we need a Systems of Particles to do so. We can apply Energy Principles such as Conservation of Energy in this situation. There is no Potential Energy, so . Our equation is:

Where is change in Kinetic Energy and is Change in the Internal Energy in A System of Particles. Since the skater moves from rest, is positive. As a result, is negative.

Lets analyze the Center of Mass of the skater.

To transform this to Work, we multiply by :

And then to from state initial to state final :

While this is similar to the Work-Energy Theorem equation, it is not exactly it. For example, and don’t represent the displacement of the point of application of the external force (the railing).

These are also not expressions of conservation of energy: the only kind of energy that appears is translational kinetic energy. We don’t include any other types of energy.

We will instead call this the Center of Mass Energy Equation.

For example, a ball rolling down an incline can be represented as:

Using conservation of energy. However, with the Center of Mass Energy Equation: