Pascal's Principle

Pascal’s Principles states that:

Pressure applied to an enclosed field is transmitted undiminished to every portion of the fluid and to the walls of the containing vessel.

If you increase the external pressure on a fluid at one location by , this change in pressure is also experienced everywhere else in the fluid.

All of hydraulics operate using Pascal’s principle. It lets us amplify small forces to move massive parts.

Proving Pascal’s Principle

We will prove Pascal’s principle for an uncompressible liquid.

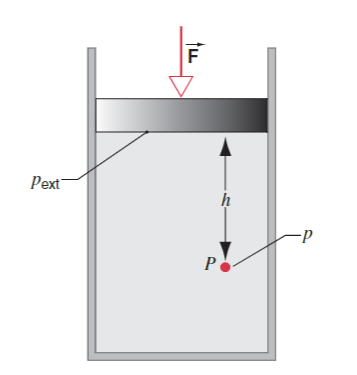
In this example, an external for is applies to a cylinder with a piston, bringing about at to the liquid inside. We can write the pressure at a point a distance below the surface:

if the external pressure is increased by , then:

Since the liquid is incompressible, does not change:

So, the change in pressure at any point in the fluid is equal to the change in external pressure, confirming Pascal’s principle.

Even though we have assumed that the liquid is incompressible in this case, Pascal’s principle is true for all fluids. For compressible fluids, a change in external pressure leads to a change in density, but the disturbance fades over time and the effect is the same.

The Hydraulic Lever

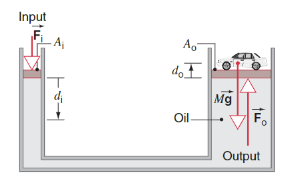
The Hydraulic Lever is an application of pascal’s principle. In this example, an external force is applied on a piston of area . On the other end, a car applies a force on a larger piston of area . In equilibrium, the two forces must be equal.

The pressure on the fluid from the small piston is , and according to Pascal’s Principle, this pressure is applied at every point in the fluid, including at the other fluid. As a result, the other fluid experiences an equal pressure, . Therefore:

Since the ratio is smaller than 1, is smaller than . When the car is lifted, the volume displaced by the movement of each liquid is the same (for an incompressible liquid).

Since the ratio is smaller than 1, similar to before, the distance moved by the large piston must be smaller than the distance moved by the small piston. Combining these equations: