Maxwell’s Equations bring the various equations for electromagnetism together in a simple and elegant way. So far we have two equations from Gauss:
An equation from Faraday:
And an equation from Ampere with Displacement Current:
Maxwell’s Equations use Curl and Divergence in Vector Fields. Essentially:
- Curl describes how vectors bend/circle. It is represented as
. - Divergence describes how the vectors spread out. We can use it as a Flux quantity; for example, how much electric flux flows out of an area. It is represented as
.
Gauss’s Law says that the electric field times an area is proportional to the charge enclosed by that area. It describes how the electric field diverges or converges from electric charges. We can write it as:
Gauss’s Law for magnetic just says that magnetic field lines are always closed loops from north to south. As a result, there is no net divergence or convergence of magnetic field — it just loops around.
Faraday’s Law says that an electric field within a loop induces a magnetic field. More specifically, electric field lines curl around changing magnetic fields.
Ampere’s law says that magnetic field will curl around currents. We then add displacement current to the end.
When we put these equations together we find that {Blanks}. Lets look at these laws for empty space with no extra fields.
Here are all the terms that don’t go to zero:
An electric field is created from a magnetic flux change and a magnetic field is created from an electric flux change. Therefore, if in empty space an electric flux is made to change over time, then a magnetic flux is created. If that magnetic flux changes with time, that creates an electric flux. This process repeats over and over again with magnetic/electric fields propagating outwards through space.
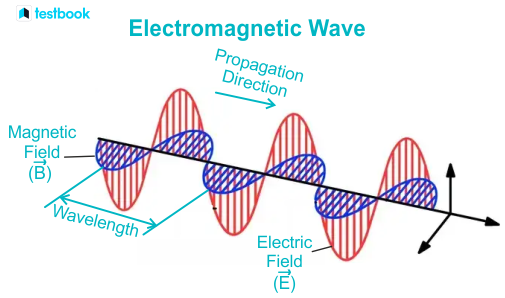This is what light is. Light is an electromagnetic wave that propagates through space as electric fields and magnetic field create one another.