Bernoulli's Equation

As an Ideal Fluid flows through a pipe or Tube of Flow, it can change in several ways:

• The cross sectional area might change.
• The inlet and outlet may be at different elevations
• The inlet and outlet pressures may be different.

Using the Equation of Continuity for fluid flow:

We related change in area to changes in velocity. Change in pressure and elevation are both related to velocity, so each type are not independent of each other.

Deriving Bernoulli’s Equation

Lets use an example of a pipe: 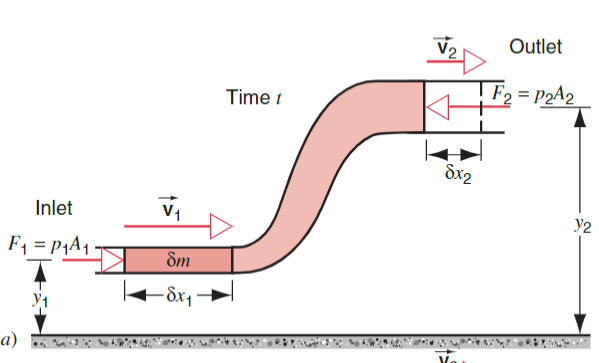The pipe has cross-sectional area and elevation at the inlet and cross-sectional area and elevation at the end. Because the area changes, the velocity changes from to .

We will use Conservation of Energy to the system of the fluid between the inlet and outlet.

Lets say that there may be a pressure from additional fluid on the left and a pressure from additional fluid on the right. This means there are forces and .

Under both forces and gravity, we will say that the system moves to the right. The figure below shows the system after a time 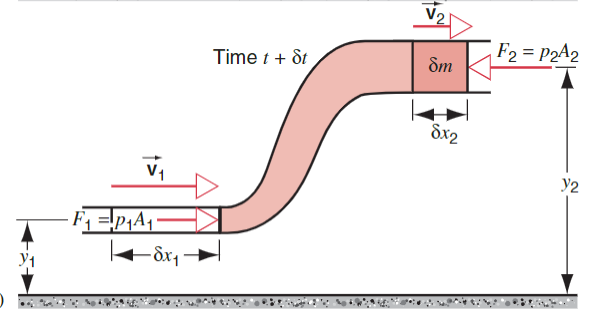. In this time, the left side has moved an and the right . These distances are different because of the difference in areas. The same effect would have been reached had we taken out the shaded section of mass from the inlet and placed it at the outlet.

There are three factors for the net External Work.

1. At the inlet, the pressure force is:

2. At the outlet, the pressure force is:

3. Work done by gravity as a fluid element moves through vertical displacement :

In Conservation of Energy, is the Potential Energy from Conservative Forces that act between objects in the system. Since our fluid is ideal, we assume there are no such forces, so .

The net external Work would be:

The volume of the shaded fluid element can be written as and , since the fluid is incompressible. The uniform and constant fluid density is and so we can also rewrite our element as . Substituting:

The change in Kinetic Energy for is:

Applying conservation of energy:

And rearranging/cancelling:

Or:

This is Bernoulli’s Equation for ideal fluids, which state that the equation above is constant along a streamline.

Analyzing Bernoulli’s Equation

As we’ve seen, Bernoulli’s Equation is a derivation of conservation of energy. We can split it into types of energies:

• is the Pressure Energy
• is the Kinetic Energy
• is the Potential Energy

Special Applications

1. Static Pressure.

Static Pressure is simply a case where velocity is 0.

Which matches the equation we derived in Variation of Pressure for Fluids at Rest.
2. Dynamic Pressure.

Suppose a fluid flowing horizontally, so there is no difference in elevation:

In this equation, as the speed is large, pressure must be small, and vice versa. The quantity is called the dynamic pressure.
3. Compressible, viscous flow.

If the fluid is compressible, then its Internal Potential Energy can change as molecules become closer and further apart.

If the flow is viscous, then the internal kinetic energy can change, similar to how Frictional forces increase the internal energy.

Our complete analysis should include internal energy:

or:

If necessary, Bernoulli’s equation could be modified to account for theses other energy transformation.

Other Applications

The Venturi Meter The Pilot Tube Dynamic Lift Thrust on a Rocket