Magnetic Force Equation
Ferromagnetic materials and particles experience a force when placed in a Magnetic Field. For an non-magnetic object to experience force from an existing magnetic material, it must:
- Have net electric charge
- Be moving
- The direction of movement cannot be parallel to the direction of the magnetic field
The magnitude of the magnetic force can be calculated using:
is the direction of the force from the magnetic field is the velocity of the positive moving charge. (for negative, use the left hand, or just have the force going the opposite direction.) is direction of the magnetic field.
Note that this definition uses the Cross Product and therefore Right-hand Rule.
In this case:
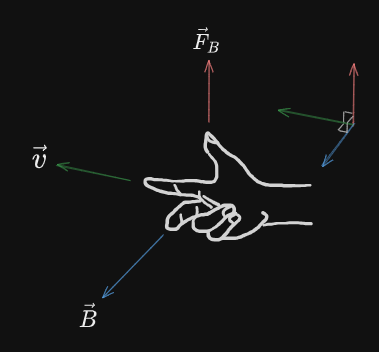
Please excuse my poorly traced hand.
An example of using this rule:
Question
For a positive charge, which direction is the force from magnetic field?
Note that in this question, the dot represents a vector out of the page. Also, an “x” represents a vector into the page.
Answer
The force is upwards for a positive charge.
Circular Motion
For a charged particle moving perpendicular to a magnetic field, the particle will move in a circle:
We can see this using the acceleration:
And by rearranging vectors to find acceleration, we can see how it points towards the center or a circle:
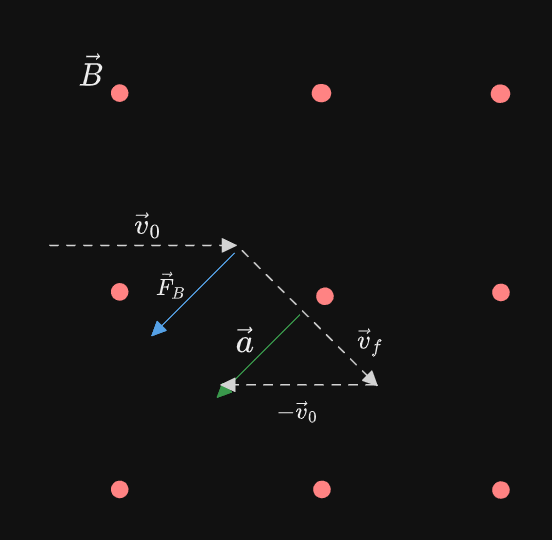
More clearly shown here:
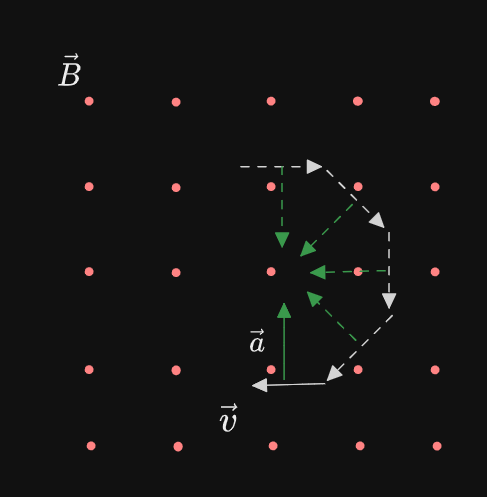
The acceleration, which changes direction but not magnitude keeps the particle in a circular path.
Note that the direction of the magnetic field is out of the page.
We can set the equations for magnetic force and centripetal force equal in this case. (Since
Giving us an equation the radius of a charged particle with the magnetic force as the centripetal force.
Info
The magnetic force never does Work on a charged particle.
- Force is perpendicular to displacement
- Because of the dot product, there is no work if the force and displacement are perpendicular.
Here is an example of these concepts in use: AP Physics C — Mass Spectrometer Question.
